《基於深度強化學習的晶片擺置》 閱讀筆記
引言
《基於深度強化學習的晶片擺置》
Google這篇一出可說語驚四座,從未有人把強化學習拿來擺physical design中的macro過。
事實上,這個步驟可說是整個flow中複雜度最高的部分之一,原因無他,所有的改變都牽一髮而動全身,要完美衡量擺放macro的效果去做決定,不能說不可能,但肯定是相當耗時的。
這時工程師真正的作用就出來了,經驗老到的可能一看就知道怎樣擺(可能)比較好,過去我們開發的演算法,可說是在用程式模擬這種經驗;而強化學習則另闢蹊徑,讓AI來扮演菜鳥工程師,從零開始學習這些know-how。
相關研究
Global placment問題是晶片設計上的一大挑戰,前人所提出的方法大致可以歸納為三個方向:基於分區、基於隨機優化、基於分析。
方法
問題定義
這份研究的課題是晶片擺置最佳化,目標是將netlist(描述晶片的graph)這張圖的節點定位在2D的有限平面上,也就是擺置空間,並且同時最佳化Power, performance and area (PPA)。
方法概覽

- states: 所有可能發生的環境的集合 (也就是所有可能產生的擺置)。
- actions: 智慧型代理人能執行的動作的集合 (也就是擺放macro到一個合法位置)。
- state transition: 給定state和action,轉場到下一個state。
- reward: 在某個state做某個動作的獎勵 (設定為零,擺完最後一步之後會用估計線長與擁擠狀況的負加權合作為獎勵。)
我們將$s_0$定義為初始state,也就是空無一物的平面,而最後的終點則是$s_T$,也就是擺放了所有Macro後完整的擺置結果。在每個單位時間$t$,智慧型代理人會觀察當前的環境$s_t$,並做動作$a_t$,以到達下一個階段$s_{t+1}$,同時獲得獎勵$r_t$ ($t<T$時為0,$t=T$時為估計的cost)。
透過重複學習這些紀錄(episodes),智慧型代理人能透過策略網路(policy network)學習最大化cost的方法。這篇論文使用Proximal Policy Optimization (PPO)的方式,來更新策略網路 $\pi_\theta(a|s)$中的參數$\theta$。
獎勵 (reward)
這篇論文的目標是最佳化PPA,而這些資訊通常是由商業tool在flow的最後產生,也就是report QoR,包含線長、繞線擁擠狀況、timing、密度、面積、power等等,這些資訊綜合在一起便是最精確的reward。然而這通常得花上數小時甚至一天的時間來產生這些結果,RL需要快速迭代的特性注定讓使用這樣的reward不現實可行,RL需要的是一個能快速估算的reward、同時足夠精確而可以代表最終的QoR。
這篇論文採用線長與繞線擁擠度來估計擺置品質,並將其加權相加後當作reward,也就是$r_t=-HPWL-c*Congestion$。
同時為了保證在足夠短的時間能算出線長,論文做了幾個假設:
- 將標準邏輯閘用hMETIS叢集起來,再用forced-directed方式來快速擺置,這使得計算線長時能獲得快速而不失精確的標準邏輯閘線長。
- 將平面離散化成數千個格子,並將macro與cell叢集的重心放置於格子的中心。
- 計算標準邏輯閘時,假設所有的線都是來自叢集中心。
- 計算繞線壅擠時,只考慮前10%嚴重的格子。
線長
HPWL,常見的估算方法,其意義可以視為是繞線長度所需的下限,大約等於其Steiner tree的線長。
這篇論文並加入一個normalize factor $q(i)$來增加估算的精確性,隨著netlist中結點的數量增加HPWL,如下所示,其中$N_{netlist}$代表netlist的數量:
$HPWL(netlist)={\displaystyle\sum_{i=1}^{N_{netlist}}q(i)*HPWL(i)}$
格子的數量
對於空白的擺置空間,有無數種格子切法可以將其離散化。而切的數量嚴重影響最佳化的複雜度與解的品質。論文將數量上限定為128x128,並將數量選擇視為一個bin-packing問題,透過浪費的格子數來衡量選擇的好壞。實驗中使用的數量平均約30。
Macro擺放順序
論文依照面積降序排列macro,並在面積相同時用topological sort來排列。
依照面積 → 避免發生無解(可擺置位置)。
topological → 使策略網路能考慮將結構相近的macro擺在一起,從而減少潛在線長。
另一種做法是在擺的同時最佳化排序,但這又使action更複雜。結果顯示以上方法可行。
標準邏輯閘擺置
採用經典的force-directed想法,將netlist類比為彈簧、用權重乘以距離來類比彈力。如此,連接比較多的會被拉的較近,線長變減少了。
此外也會加入將重疊的cell分開的力。
為了避免震盪,會限制每次移動的距離。
force-directed可以參考這篇。
繞線壅擠
論文參考這篇建立congestion map,並用5X1的卷積來平滑結果。
所有net繞線完後,會選取前10%嚴重的數值套用進獎勵的計算式裡。
密度
論文將格子中的使用率也就是密度當作限制,禁止策略網路將macro放在密度超過最大值($max_{density}$)的格子中、也就是可能產生重疊的格子。
這個做法有兩個好處:
- 減少策略網路產生的非法解。
- 減小解空間、降低複雜度。
可行的標準邏輯閘擺置應該符合以下限制:不得超過最大密度($max_{density}$)。這個值在實驗中被設為0.6。
為了符合這些限制,論文準備了一個$m \times n$的boolean矩陣、表示該格是否滿足限制,將這個矩陣乘上策略網路的輸出,便能把不合限制的位置去除。
如果要加入blockage也很單純,將該格的限制矩陣設為0即可。
評估擺置品質前處理
論文會用類似tetrix的想法把macro放到最近的合法位置,之候固定macro後用商業tool去擺標準邏輯閘以取得最終的QoR。
action的表示
前面描述過論文將擺置空間化為$m \times n$的格子,策略網路的輸出便會是$m \times n$的機率分佈,動作會選擇最高的位置來擺放macro。
state的表示
論文使用netlist的圖(相鄰矩陣)、點的資訊(寬、高、種類…等等)、邊的資訊(連接數量)、當前擺的macro、其連接資訊、整體資訊(繞線資源、線的數量、macro與標準邏輯閘叢集的資訊等等)表示一個state。
論文接下來會討論如何有效處理這些資訊,以學習擺置。
基於經驗學習更好擺置
擺置的目標式可以定義如下:
$J( \theta ,G )=\dfrac{1}{K}\displaystyle\sum_{g \sim G}^{}
E_{g,p\sim\pi_{\theta}}[R_{p,g}]$
$\theta$是策略網路的參數,$G$是大小為$K$的netlist,個別net由$g$來表示,$R_{p,g}$代表一個章節中的某個擺置$p$裡、某net $g$的獎勵,也就是:
$$
\begin{split} R_{p,g}=-Wirelen >h(p,g)-\lambda \ Congestion(p,g) \cr
&S.t.density(p,g)\leq max_{density} \end{split}$$
這個式子便是論文中的最佳化目標,$\lambda$被設為$0.01$、$max_{density}$則為$0.6$。
藉由監督式學習來轉移經驗
移植策略網路很有挑戰性,因為擺置內容千變萬化。論文首先嘗試學習多種不同的擺置,因為一個能擺出最佳解的網路應該能有效地理解擺置的資訊──即使換了不一樣的擺置。因此論文便提出了要訓練預測獎勵的網路,來當作策略網路的解碼器。(結果還是得搞一堆測資嗎※。)
為了訓練,論文找了五個加速器架構、每個產生2000種擺置,共10000筆當作訓練資料。產生的方法便是讓一個原始的策略網路亂擺,並給予不同的參數。一開始網路會產生一些低品質擺置,但隨著網路訓練,品質會逐漸改善,因此可以收集到多樣的資料。
論文中設計圖神經網路(graph neural network)架構來解碼netlist的資訊,主要作用就是將一個很大的超圖編碼成可處理的向量,方便策略網路去理解。類似的例子可以參考分類圖中點、擺device、預測連結性與預測DRC。(別人的筆記,有空看個)
點的表示會將其資訊串接成vector,隨著相鄰矩陣輸入進網路。
點($v_i$)與邊($e_{ij}$)會進行如下的更新:
$$\begin{alignedat}{2} e_{ij} &= &fc_1(concat(fc_0(v_i)|fc_0(v_j)|w^e_{ij})) \cr
v_i &= &mean_{j \in \mathcal{N}(v_i)}(e_{ij}) \end{alignedat}
$$
兩者的embedding會隨機初始化,維度是32-D。$fc_0$為$32 \times 32$、$fc_1$為$65\times 32$的前饋網路,$w^e_{ij}$為$1\times 1$的可學習權重。$\mathcal{N}(v_i)$代表$v_i$的鄰居。
策略網路架構
下圖展示策略網路(${\pi}_{\theta}$)與價值網路的架構:
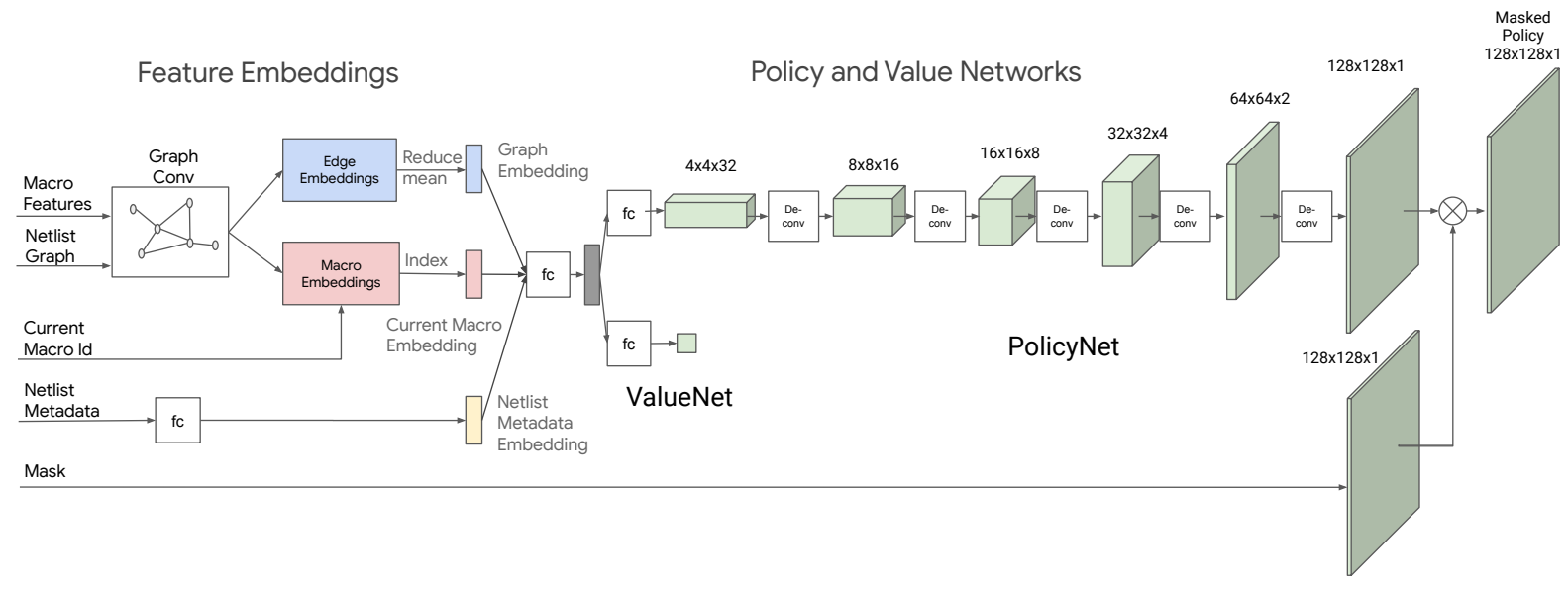
將前述的監督式學習拔掉預測層拿來當編碼器,並加入背景資訊。輸出經過反捲積、batch normalize,產生最終的機率分布。機率分布還會與遮罩內積,去除掉不合法的位置。
策略網路($\theta$值)的訓練
使用Proximal policy optimization (PPO)來更新,參照這篇。
結果
經過預先訓練的策略網路在遇到沒碰過的case時(訓練12hr),表現明顯優於未預訓練的(訓練24hr)。顯示預訓練的網路能有效傳承經驗。
網路之後使用更大的資料集(2→5→20 blocks)進行訓練,有效減少了過擬合,表現也更好。
論文與SA、RePlAce、手擺做比較。
SA當然是被打趴(線長&擁擠度),畢竟是老方法。
RePlAce與人工擺則是值得玩味。人擺出的結果在擁擠度這項指標優於另兩者,在timing方面也不錯,但人工擺置來自於長達數周的反覆試誤,而RL則只需要3-6小時來調整。RePlAce所需時間更短(1-3.5小時),但RePlAce並未顯著地改善擺置的timing,這可能是因為沒有考慮繞線擁擠所導致。
論文最後討論了改善方向,其中一個重點會是增進標準邏輯閘快速擺置的精確性。此外也可以考慮將RL的做法往其他階段延伸,例如合成。\
(不過,對於這樣的比較,也有些人有不同的看法。看起來這篇論文似乎也有難以重現的問題。
結論
論文提出RL擺置的方法,可以在6小時內產生品質相近於人類數周的成果。相信AI未來會是輔助APR的重要工具。